14 Sortering
Väldigt ofta måste data sorteras för att kunna vara hanterbart. Det kan röra sig om att sortera t.ex. tal, datum eller ord i storleksordning, stigande/fallande ordning eller bokstavsordning. Syftena med att programmera sortering kan vara många men inte sällan handlar det om att enklare kunna söka (nästa kapitel) efter information, oavsett om det rör sig om en människa eller en dator.
Eftersom att sortering är ett så pass vanligt förekommande problem inom programmeringen finns massor av algoritmer utvecklade för att lösa det. De är olika effektiva i olika situationer (storlek och typ av data) och det är svårt, åtminstone inom ramen för denna kurs att lära sig allihop. Däremot bör man lära sig minst en algoritm för att kunna förstå principen bakom hur en dator sorterar. För att göra det hela begripligt kommer vi till en början att nöja oss med att sortera tal som är organiserade i arrayer.
14.1 Insertion sort
En av alla sorteringsalgoritmer som finns heter insertion sort (eller infogande sortering på svenska). Vi studerar just denna algoritm eftersom att den har en bra avvägning mellan att vara enkel att förstå och effektiv väldigt många fall. Strukturdiagrammet för algoritmen ser ut såhär:
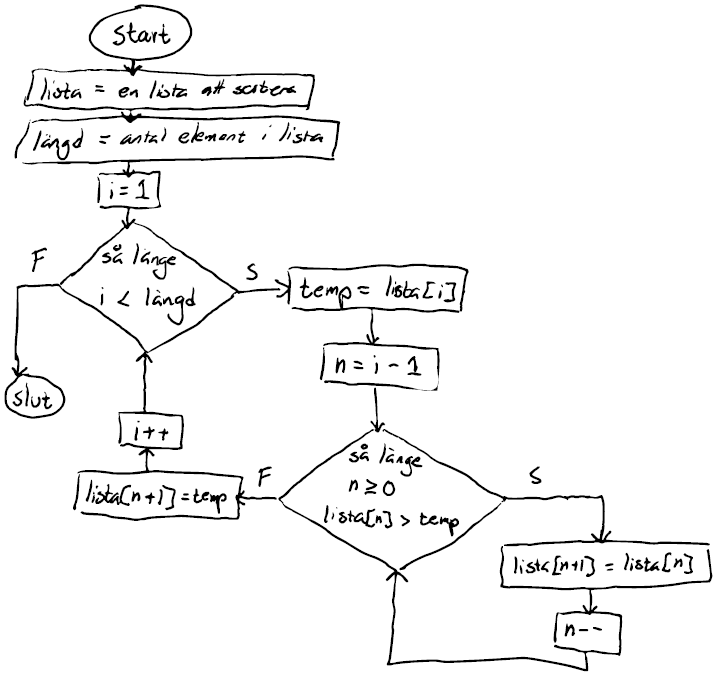
Strukturdiagram för insertion sort.
Ovanstående diagram ger oss pseudokoden för insertion sort:
start
lista = en lista att sortera
längd = antal element att sortera i lista
i = 1
så länge i < längd
temp = lista[i]
n = i - 1
så länge n >= 0 & lista[n] > temp
lista[n + 1] = lista[n]
n--
lista[n + 1] = temp
i++
slutKortfattat kan man säga att algoritmens teknik för att sortera går ut på att plocka ut ett tal i taget och stoppa in det (infoga) på rätt plats. På sidan 191 i boken finns en enkel steg för steg-beskrivning som gör det lite klarare. En ännu bättre förklaring finner du dock på visualgo.net/en/sorting om du sedan klickar på INS i menyn längst upp. Där kan du starta en animering som visar vad som sker i varje steg. Du kan även pausa och manuellt stega både framåt och bakåt.
Om vi istället tittar på källkod så kan insertion sort skrivas såhär i C#:
int[] lista = { 3, -5, 7, 38, 1, 0, 23, 15 };
for (int i = 1; i < lista.Length; i++)
{
int temp = lista[i];
int n = i - 1;
while (n >= 0 && lista[n] > temp)
{
lista[n + 1] = lista[n];
n--;
}
lista[n + 1] = temp;
}Det är ofta en bra idé att göra en utskrift av listan både före och efter sortering så att man enkelt kan kontrollera sin algoritm. Detta göras smidigast med en utskrifts-metod.
public static void Main()
{
int[] lista = { 3, -5, 7, 38, 1, 0, 23, 15 };
SkrivUtLista(lista);
for (int i = 1; i < lista.Length; i++)
{
int temp = lista[i];
int n = i - 1;
while (n >= 0 && lista[n] > temp)
{
lista[n + 1] = lista[n];
n--;
}
lista[n + 1] = temp;
}
SkrivUtLista(lista);
}
static void SkrivUtLista(int[] lista)
{
for (int i = 0; i < lista.Length; i++)
{
Console.Write(lista[i] + " ");
}
Console.WriteLine();
}Självklart är det också en god idé att placera sin sorteringsalgoritm i en egen metod. Det kan ju mycket väl vara så att den behöver användas flera gånger eller på olika arrayer. Kom ihåg att array som parameter hanteras som referens och du behöver därmed ej returnera något - förändringarna i metoden sker även i orginalarrayen.
public static void Main()
{
int[] lista = { 3, -5, 7, 38, 1, 0, 23, 15 };
SkrivUtLista(lista);
SorteraInfogade(lista);
SkrivUtLista(lista);
}
static void SorteraInfogade(int[] lista)
{
for (int i = 1; i < lista.Length; i++)
{
int temp = lista[i];
int n = i - 1;
while (n >= 0 && lista[n] > temp)
{
lista[n + 1] = lista[n];
n--;
}
lista[n + 1] = temp;
}
}
static void SkrivUtLista(int[] lista)
{
for (int i = 0; i < lista.Length; i++)
{
Console.Write(lista[i] + " ");
}
Console.WriteLine();
}14.2 Bubble sort
Den sorteringsalgoritm som många elever/studenter ofta får lära sig allra först är bubble sort (eller bubbelsortering). Den må vara relativt enkel att förstå men den är i väldigt många fall ineffektiv och därav sällan användbar. Det är dock inte så dumt att bekanta sig med bubble sort för att i nästa del kunna resonera om algoritmers effektivitet.
Den generella principen bakom bubble sort är att jämföra talen i de två första elementen, byta plats om de sitter i fel ordning, jämföra nästa två tal, byta plats om de sitter i fel ordning och sedan upprepa denna procudur tills hela listan har gåtts igenom en gång (ett tal kommer då finnas på rätt plats). Därefter behöver upprepningar av hela procudren ske igen tills dess att hela listan är sorterad, dvs till vi har fått alla tal på rätt plats (du kan även se en animering för bubble sort på visualgo.net/en/sorting, välj BUB i menyn längst upp). Vi illustrerar i vanlig ordning med ett strukturdiagram:
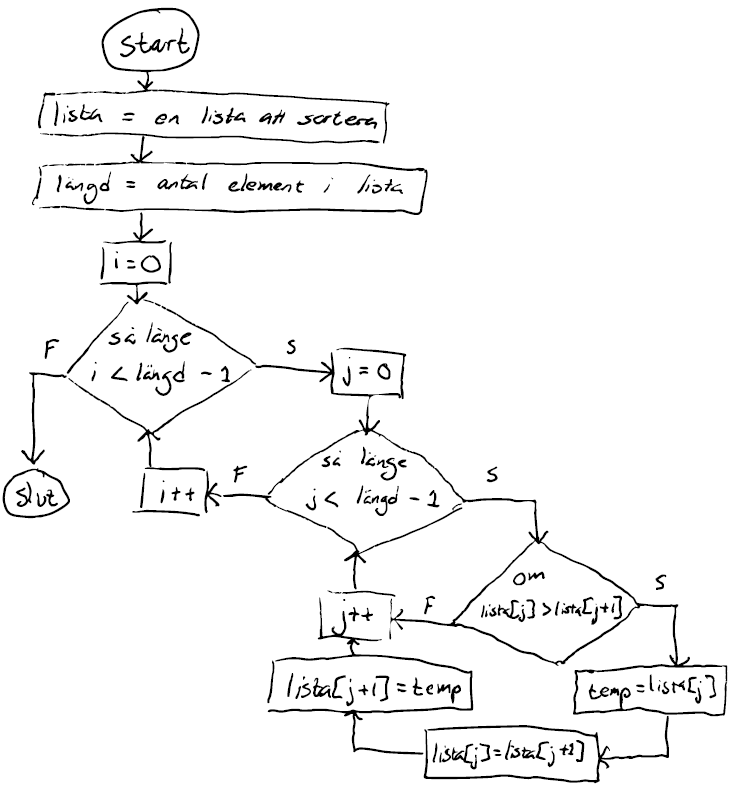
Strukturdiagram för bubble sort.
Pseudeokoden för detta diagram ser ut såhär:
start
lista = en lista att sortera
längd = antal element i lista
i = 0
så länge i < längd - 1
j = 0
så länge j < längd - 1
om lista[j] > lista[j + 1]
temp = lista[j]
lista[j] = lista[j + 1]
lista[j + 1] = temp
j++
i++
slutOm vi implementerar algoritmen i C# ser den något enklare ut eftersom att vi då kan dra nytta av for-satsen vilket gör att koden för våra loopar kan skrivas något enklare:
int[] lista = { 3, -5, 7, 38, 1, 0, 23, 15 }
for (int i = 0; i < lista.Length - 1; i++)
{
for (int j = 0; j < lista.Length - 1; j++)
{
if (lista[j] > lista[j + 1])
{
dobule temp = lista[j];
lista[j] = lista[j + 1];
lista[j + 1] = temp;
}
}
}Givetvis är det god idé även för denna algoritm (och för de allra flesta) att göra utskrifter före och efter samt plocka ut algoritmen till en egen metod, men det kan du nu så vi tar inte med det steget en gång till!
Den algoritmbeskrivning av bubble sort som finns ovan kan optimeras på två olika sätt. Dels vet vi att efter ett varv i den yttre loopen kommer vi inte behöva gå igen hela lista i den inre loopen. Dessutom kan vi vara säkra på att om inget byte alls sker under ett varv så måste hela listan redan vara sorterad och vi kan avbryta. Mer om detta i en kommande övning.
14.3 Tidskomplexitet
En algoritms tidsåtgång (eller egentligen antalet operationer datorn behöver göra) som funktion av indatats storlek kan växa på olika sätt för olika algoritmer. Vid små datamängder ser vi ingen skillnad men för stora indata kan en snabbt växande tidsåtgång bli ett stort problem.
Ju större datamängder vi tittar på desto mer dominant blir bidraget till resultatet från en viss term i ett uttryck. Om vi t.ex. tittar på
\[ f(x) = x^2 + 3x \]
och undersöker \(x = 100000\) så får vi
\[ f(100000) = 100000^{2} + 3*100000 = 10^{10} + 3*10^{5} = 1.00003*10^{10} \]
Bidraget till funktionens värde då \(x = 100000\) från termen \(x^{2}\) är alltså mycket större än det från termen \(3x\) och detta växer givetvis med större värden på \(x\).
Om vi ska resonera kring funktionsvärdet är det alltså den starkast bidragande termen som är mest intressant. Till och med i sådan utsträckning att vi nöjer oss med att endast titta på den termen. Dessutom förenklar vi bort eventuella koefficienter. Vi närmar oss då (något omatematiskt) det matematiska begreppet ordo, O (eng: Big O-notation). När vi pratar om indata så håller vi oss till heltal (vi kan ju t.ex. inte ha en halv extra position i en array) och därför brukar man använda \(n\) som variabel snarare än \(x\). Om den starkast bidragande termen är kvadratisk (som i exemplet ovan) skriver man då
\[ O(n^{2}) \]
och detta utläses ordo n-kvadrat och inte som O av n-kvadrat som man kanske är van vid då det liknar skrivsättet \(f(x)\). Man säger alltså att funktionen \(f(n) = n^{2} + 3n\) har ordo \(n^{2}\). Några fler exempel:
| Funktion | Ordo |
|---|---|
| \(3n^2\) | \(O(n^2)\) |
| \(3n^2 -7\) | \(O(n^2)\) |
| \(5n\) | \(O(n)\) |
| \(13n^3 + 2n^2\) | \(O(n^3)\) |
| \(2^n + n^2\) | \(O(2^n)\) |
| \(5\) (konst.) | \(O(1)\) |
Om vi ritar flera olika typer av kurvor i ett och samma diagram och fortfarande minns att ordo beskriver tidsåtgång (tidskomplexitet) så kan vi ganska lätt inse att algoritmer som har olika ordo kan ha väldigt stor skillnad i effektivitet när vi pratar om tillräckligt stora värden på indata.
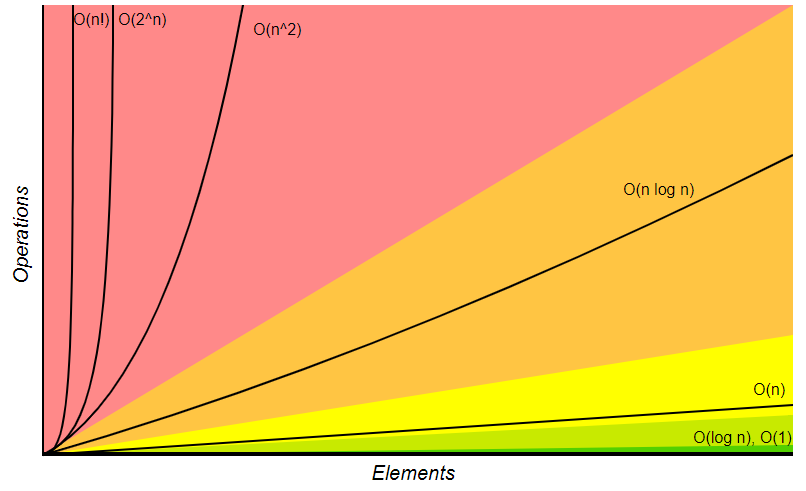
Graf över olika ordo.
En bra sammanfattning över ordo för olika algoritmer finns på bigocheatsheet.com.
14.3.1 Exempel: Sortera Facebook-användare
Enligt svenska Wikipedia hade Facebook två miljarder ( \(2.9 * 10^9\) ) aktiva användare 2017. Om det skulle vara så att vi behöver sortera alla användares ID skulle det bli rejäla skillnader i tidsåtgång beroende på vilken sorteringsalgoritm vi använder. Om vi först provar med bubble sort som har \(O(n^2)\). Antalet operationer datorn behöver göra blir:
\[ O(n^{2}) \Rightarrow {2*10^9}^2 = 4*10^{18} \]
En dator som inte är allt för trött idag kan utföra ungefär 150000 MIPS (IPS = instruktioner per sekund), dvs \(150000*10^6 = 1.5*10^11\) IPS. Tiden för sortering med en sådan dator blir då:
\[ \frac{4*10^{18}}{1.5*10^{11}} = 2.67*10^7 s = 7400 h = 310 dygn \]
Om vi istället skulle använda t.ex. merge sort (som har \(O(n*log(n))\) ) skulle beräkningen istället bli:
\[ O(n * log_2(n)) \Rightarrow 2*10^9 * log_2(2*10^9) = 6.18 * 10^{10} \]
\[ \frac{6.18*10^{10}}{1.5*10^{11}} = 0.4 s \]
Från 310 dygn till 0,4 s - valet av algoritm kan alltså spela väldigt stor roll!
14.4 Övningar
-
Mätningar på Bubble sort:
- Utgå från den Bubble sort-kod som finns tidigare i kapitlet och utöka med/genomför följande.
- Lägg utskrift av arrayen i egen metod. Anropa metoden före och efter sortering för att kontrollera att sorteringsalgoritmen beter sig korrekt.
- Lägg Bubble sort-algoritmen i egen metod. Anropa metoden från huvudprogrammet. Testkör igen och kontrollera så att ingen funktionalitet har förlorats.
- Lägg till direktivet
using System.Diagnostics;längst upp i källkoden. - Skapa en ny variabel av typen
Stopwatchmed kodradenStopwatch timer = new Stopwatch(); - Kör
timer.Start();precis före sorteringsanropet ochtimer.Stop();precis efter. - Skriv ut tiden för sortering med hjälp av
timer.ElapsedMilliseconds. - Ändra storleken på arrayen till
1000och låt talen som slumpas fram vara inom spannetint.MinValueochint.MaxValue. - Kör programmet och notera tiden det tar att sortera samt storleken på arrayen. Upprepa samma körning tre gånger och beräkna medelvärdet av tiden. Fyll i storleken och medelvärdet i ett kalkylblad i Excel.
- Upprepa proceduren (med tre körningar per storlek och sedan ta medelvärdet) för storlekarna:
2500,5000,7500,10000,20000,30000,40000och50000. Notera samtliga i ditt kalkylblad. - Använd Excel för att göra ett punktdiagram och anpassa en kurva för dina värden. Vilken typ av kurva ger bäst matchning (störst $ R^2 $-värde)?
- Försök att göra följande optimeringar av algoritmen för Bubble sort:
- När ett varv har genomförts vet vi att det sista elementet är på rätt plats. Det behöver inte kontrolleras igen vid nästa varv. Med andra ord behöver vi inte gå igenom hela arrayen vid varje varv. Redigera din kod så att dessa onödiga kontroller ej behöver göras.
- Om ett varv, vilket som helst, inte behöver byta plats på några element alls så måste hela arrayen vara sorterad. Vi kan då avbryta algoritmen i förtid och slippa köra resten av den. Redigera din kod så att den minns om ett byte har gjorts eller inte, om inte så avbryts algoritmen.
- Testa din sortering (med hjälp av utskrift) igen för att försäkra dig om att den fortfarande fungerar som tänkt.
- Gör om några av mätningarna av exekveringstid, märks någon skillnad?
- Redigera din Bubble sort-kod så att den sorterar fallande istället för stigande. Testa med hjälp av utskrift så att den gör rätt.
Genomför övningen Save Patients som finns på ett separat blad (laddas ned på lärplattformen).
-
Skriv ett program som slumpar fram 20 heltal i en array. Låt användaren bestämma om talen i arrayen ska sorteras i stigande eller fallande ordning. Implementera insertion sort och sortera utifrån det val användaren har gjort.

Sortering i fallande ordning med insertion sort.
Skriv ett program där 20 decimaltal slumpas till en array. Sortera första halvan av arrayen i stigande ordning och andra halvan i fallande ordning. Du bestämmer själv vilken sorteringsalgoritm du utgår ifrån.