15 Sökning
I förra kapitlet nämndes att en av de vanligaste anledningarna till att sortera något är att enklare kunna göra en sökning. Givetvis är det möjligt att söka i en datamängd som inte är sorterad - det är ju helt enkelt bara att titta på varje element, från början till slut tills dess att vi funnit det vi söker efter. En sådan enkel algoritm kan vi beskriva med följande strukturdiagram och pseudokod:
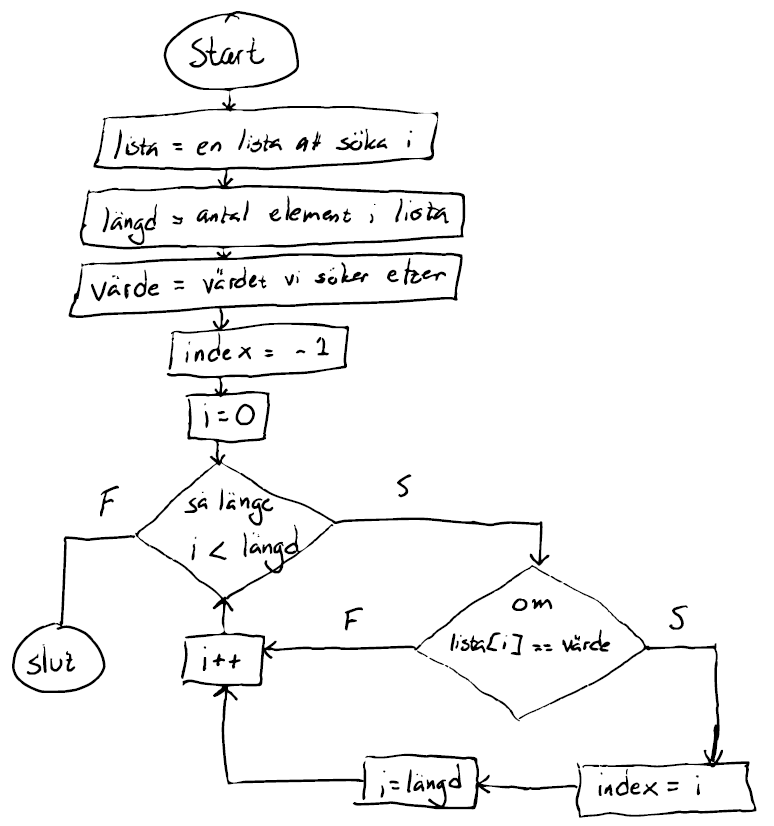
Strukturdiagram för sekventiell sökning.
start
lista = en lista att söka i
längd = antal element i lista
värde = värdet vi söker efter
index = -1
i = 0
så länge i < längd
om lista[i] == värde
index = i
i = längd
i++
slutGör vi en implementation i C# ser det ut såhär (att sätta i = längd innebär att vi vill avbryta, därav break i källkoden nedan):
int[] lista = { 3, -5, 7, 38, 1, 0, 23, 15 };
int varde = 23;
int index = -1;
for (int i = 0; i < lista.Length; i++)
{
if (lista[i] == varde)
{
index = i;
break;
}
}Att vi sätter index = -1 från början innebär att vi själva har definierat att -1 betyder att vi inte hittat det sökta talet i arrayen. Om vi ska snygga till strukturen på vår algoritm lite så lägger vi den i en egen metod och låter den metoden returnera det index som vi finner det sökta talet på, dvs vår index-variabel. Då ser i så fall ovanstående kod ut såhär:
static int SekventiellSokning(int[] lista, int varde)
{
int index = -1;
for (int i = 0; i < lista.Length; i++)
{
if (lista[i] == varde)
{
index = i;
break;
}
}
return index;
}Denna algoritm kallar vi för sekventiell sökning (eller ibland enkel sökning) och kan alltid användas för att hitta vad som helst i vilken datamängd som helst. Däremot är den inte särskilt effektiv jämfört med nästa sökalgoritm - binär sökning!

Sekventiell sökning kan bli outhärdlig.
15.1 Binär sökning
Du kanske minns leken där en person tänker på ett tal (t.ex. mellan 1 och 100) och en annan skall gissa vilket tal man tänker på. Vid varje felgissning får man reda på om man gissat på ett för stort eller för litet tal. Givetvis kan man ha tur och gissa rätt med en gång om man tar ett tal på måfå men tricket för att i det generella fallet minimera antalet gissningar är att hela tiden gissa på talet i mitten. Eftersom att vi får reda på om vi gissat för stort eller för litet kan vi redan efter första gissningen utesluta hälften av alla möjliga tal.
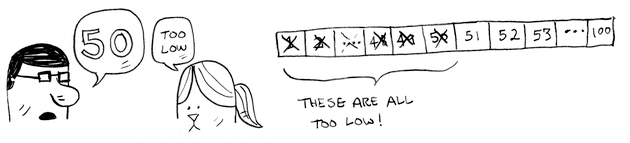
Binär sökning utesluter hälften av möjligheterna direkt.
Om man sedan upprepar denna procedur för den del av talen som är kvar (gissa på nya mitten) så har vi en konceptuell beskrivning för en algoritm som hittar det vi söker efter. Vi halverar sökmängden vid varje gissning (varje varv i vår algoritm):

Relativt få upprepningar med binär sökning behövs för att hitta rätt svar.
Som strukturdiagram och pseudokod ser algoritmen ut som följer.
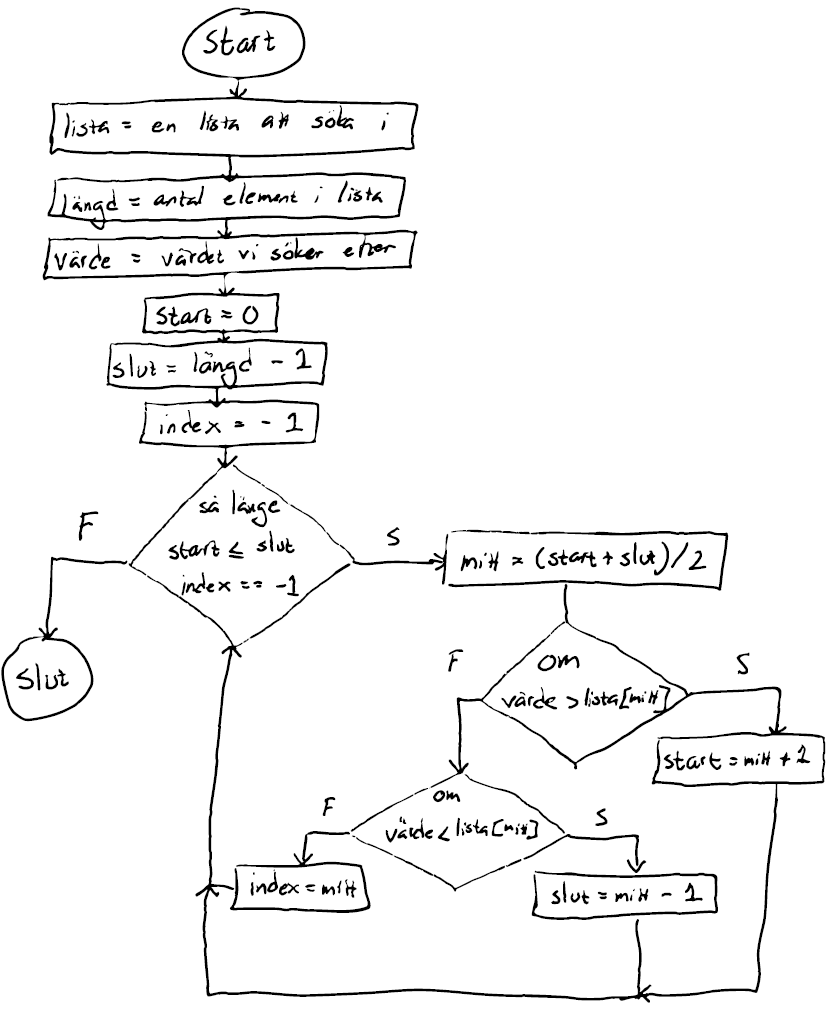
Strukturdiagram för binär sökning.
start
lista = en lista att söka i
längd = antal element i lista
värde = värdet vi söker efter
start = 0
slut = längd - 1
index = -1
så länge start <= slut & index == -1
mitt = (start + slut) / 2
om värde > lista[mitt]
start = mitt + 1
annars om värde < lista[mitt]
slut = mitt - 1
annars
index = mitt
slutGör vi en implementation av denna i C# (som egen metod) får vi följande källkod:
static int BinarSokning(int[] lista, int varde)
{
int start = 0;
int slut = lista.Length - 1;
int index = -1;
while (start <= slut && index == -1)
{
int mitt = (start + slut) / 2;
if (varde > lista[mitt])
{
start = mitt + 1;
}
else if (varde < lista[mitt])
{
slut = mitt - 1;
}
else
{
index = mitt;
}
}
return index;
}Var dock noga med att lägga på minnet att denna typ av sökning kräver en sorterad datamängd. Du kan se en animering över hur de två olika sökalgoritmerna jobbar på cs.usfca.edu/~galles/visualization/Search.html.
15.2 Effektivitet
Givetvis skall man ha i åtanke att det tar en viss tid att sortera en datamängd innan man blint hoppar på binär sökning. Men om vi gör några enkla exempelberäkningar med hjälp av ordo för sekventiell och binär sökning inser vi att det lönar sig ganska snabbt med binär sökning om mer än sökning skall genomföras i samma datamängd (den behöver ju bara sorteras en gång).
Sekventiell sökning har \(O(n)\) och binär sökningar har \(O(log_2(n))\). Vi tittar återigen på worst case (och avrundar uppåt) får nedanstående, enorma skillnad.
| Antal element | Antal operationer: \ Sekventiell sökning | Antal operationer: \ Binär sökning |
|---|---|---|
| 100 | \(1*10^2\) | \(7\) |
| 10 000 | \(1*10^4\) | \(14\) |
| 1 000 000 000 | \(1*10^9\) | \(30\) |
15.3 Övningar
OBS! Om du har en bok med upplaga från 2012 så är de fel som nämns i uppgift 5 och 6 tillrättade. Du kan därmed hoppa över dessa. Om din bok är äldre än 2012 är det bara köra på som vanligt.
Studera källkoden till sekventiell sökning på s. 195 i boken. Ett fel har letat sig in där. Kan du hitta det?
Studera källkoden till binär sökning på s. 197 i boken. Tre fel (utöver den märkliga indentering av if-satserna) har letat sig in där. Kan du hitta alla tre?
Hur många varv behöver en binär sökalgoritm gå för att garanterat hitta ett tal i en sorterad mängd med 150 element?
Implementera en sekventiell sökning genom att endast titta på strukturdiagrammet eller pseudokoden i kapitlet (inte C#-koden).
Implementera en binär sökning genom att endast titta på strukturdiagrammet eller pseudokoden i kapitlet (inte C#-koden). Återanvänd dig av någon av sorteringsalgoritmerna från förra kapitlet.
15.4 Fördjupning: Sortering/sökning med strängar
Hittills har vi nöjt oss med att sortera/söka efter heltal och vi kan göra likadant med decimaltal. Däremot behöver vi lite nya knep om vi ska sortera strängar. Studera dokumentationen för String.CompareTo() på docs.microsoft.com/en-us/dotnet/api/system.string.compareto?view=netframework-4.7.2#System_String_CompareTo_System_String_ och genomför sedan nedanstående uppgifter.
Skriv ett program där användaren får mata in flera ord på en och samma rad. Placera varje ord i varsitt element i en strängarray (använd
Split). Sortera sedan denna array i bokstavsordning och skriv ut till användaren. Använd valfri sorteringsalgoritm.-
Skriv ett program som hanterar en highscore-lista. Användaren får skriva in tio olika rader med namn och poäng (separerade med mellanslag) och dessa placeras i varsin array. Sortera arrayen med poäng i fallande ordning och gör samtidigt samma förändringar i namn-arrayen (så att den blir sorterad på samma sätt som poängarrayen).
Utöka programmet så att man kan söka upp vem som har en viss poängsumma. Använd binär sökning.
Går det göra en binär sökning på namn istället (så att man får reda på hur många poäng den eftersökte spelaren har)? Varför/varför inte?
Genomför de eventuellt nödvändiga förändringarna för att man som användare ska kunna söka efter namn istället för poäng.
Går det skriva programmet så att användaren har möjlighet att söka både på namn och på poäng? Vad krävs då i så fall?